Solution #4 - Connection Matrices

[MATLAB logo] Exploiting MATLAB's Data Structures

Solution #4 - Connection Matrices

In addition to their typical use solving large systems of equations that involve only few non-zero terms, sparse matrices are useful for storing connection matrices. A connection matrix is a matrix that contains a non-zero value (typically 1) at the intersection of a row and column that are related somehow. For instance, suppose you have three pins that are connected together by directed strings so as to create a triangular graph.

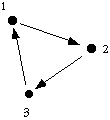
The connection matrix for this situation is

0 0 1

1 0 0

0 1 0

The rows and columns of a connection matrix can refer to different things (unlike the example above) . An example of this is the connection matrix for the Delaunay triangularization that relates pixel number to triangle number. There is a one in the connection matrix if a given pixel (row index) is part of a particular triangle (column index).

If you multiply connection matrices, the result is a connection matrix that relates the new rows to new columns. For instance, if you multiply the connection matrix for the triangle above by itself you get the connection matrix that relates the pins that are connected by two jumps.

0 1 0

0 0 1

1 0 0

It is not evident in these 3-by-3 examples but you can imagine that the connection matrix for more complicated situations might have a lot of zeros in them. This is where sparse matices come in. A sparse matrix is a very efficient way of storing a connection matrix.

Goal: Create the connection matrix that shows which triangles share a common side.

Key concepts: connection matrices, sparse matrices,

Key functions: delaunay, trisurf, sparse

Solution

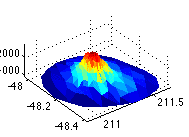
The file seamount.mat contains data from measurements of the depths of a seamount relative to sea level. The variables x and y contain the position of each measument.
Load the dataset and use the function delaunay to compute the Delaunay triangulation tri for the (x,y) points. The Delaunay tringularization is a "nice" triangularization that produces triangles that are as equilateral as possible.
load seamount
tri = delaunay(x,y);
Display the surface using the trisurf command.
trisurf(tri,x,y,z)
Now create the connection matrix C that relates the measuremnt number (rows) to the triangle number (columns). Use the order in the x,y vectors and tri for the numbering. C = sparse(tri,repmat((1:size(tri,1))',1,3),1);
What this says is create a sparse matrix with ones in rows defined by the elements in tri and in columns defined by the triangle number each element is from. The call to repmat produces a matrix that looks like

1 1 1

2 2 2

3 3 3

4 4 4

and so on (this is the matrix of triangle numbers). To look at the structure of this matrix use spy(C).

What is the connection matrix C'*C?

The connection matrix C'*C is the triangle-to-triangle connection matrix. It shows which triangles share a common side.